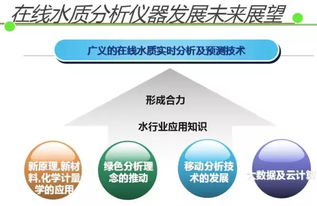
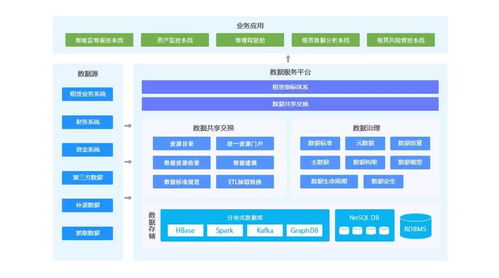
图是一种重要的非线性数据结构,广泛应用于社交网络、路径规划、网络拓扑等领域。在C语言中,图的数据处理涉及图的表示、遍历、最短路径、最小生成树等核心算法。本文将介绍C语言中图的基本表示方法及常见数据处理技术。
一、图的表示方法
在C语言中,图通常有两种表示方法:邻接矩阵和邻接表。
1. 邻接矩阵
邻接矩阵使用二维数组表示图中顶点之间的边关系。对于具有n个顶点的图,可以定义一个n×n的矩阵。如果顶点i到顶点j有边,则矩阵元素a[i][j]为1(无权图)或边的权重(有权图);否则为0或无穷大。
`c
#define MAX_VERTICES 100
#define INF 99999
typedef struct {
int vertices;
int matrix[MAXVERTICES][MAXVERTICES];
} Graph;`
2. 邻接表
邻接表使用链表数组表示图,每个顶点对应一个链表,链表中存储与该顶点相邻的顶点信息。邻接表适用于稀疏图,节省存储空间。
`c
typedef struct AdjListNode {
int dest;
int weight;
struct AdjListNode* next;
} AdjListNode;
typedef struct {
AdjListNode* heads[MAX_VERTICES];
int vertices;
} GraphList;`
二、图的遍历算法
图的遍历是许多图算法的基础,主要包括深度优先搜索(DFS)和广度优先搜索(BFS)。
1. 深度优先搜索(DFS)
DFS采用递归或栈实现,沿着图的深度方向遍历顶点。
void DFS(Graph* g, int start, int visited[]) {
visited[start] = 1;
printf("%d ", start);
for (int i = 0; i < g->vertices; i++) {
if (g->matrix[start][i] && !visited[i]) {
DFS(g, i, visited);
}
}
}2. 广度优先搜索(BFS)
BFS使用队列实现,按层次遍历图的顶点。
void BFS(Graph* g, int start, int visited[]) {
int queue[MAX_VERTICES], front = 0, rear = 0;
visited[start] = 1;
queue[rear++] = start;
while (front < rear) {
int current = queue[front++];
printf("%d ", current);
for (int i = 0; i < g->vertices; i++) {
if (g->matrix[current][i] && !visited[i]) {
visited[i] = 1;
queue[rear++] = i;
}
}
}
}三、最短路径算法
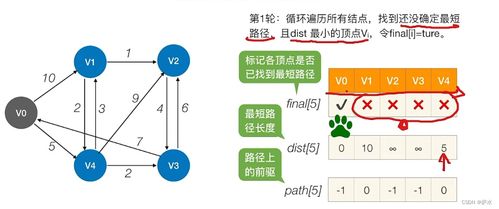
最短路径算法用于寻找图中两个顶点之间的最短路径,常见算法有Dijkstra算法和Floyd-Warshall算法。
1. Dijkstra算法
Dijkstra算法适用于有权图(权重非负),使用贪心策略求解单源最短路径。
void Dijkstra(Graph* g, int src, int dist[]) {
int visited[MAX_VERTICES] = {0};
for (int i = 0; i < g->vertices; i++) {
dist[i] = INF;
}
dist[src] = 0;
for (int count = 0; count < g->vertices - 1; count++) {
int u = -1;
for (int i = 0; i < g->vertices; i++) {
if (!visited[i] && (u == -1 || dist[i] < dist[u])) {
u = i;
}
}
visited[u] = 1;
for (int v = 0; v < g->vertices; v++) {
if (!visited[v] && g->matrix[u][v] && dist[u] + g->matrix[u][v] < dist[v]) {
dist[v] = dist[u] + g->matrix[u][v];
}
}
}
}四、最小生成树算法
最小生成树用于在连通加权图中找到权值和最小的树,常见算法有Prim算法和Kruskal算法。
1. Prim算法
Prim算法从任意顶点开始,逐步添加最小权重的边,直到包含所有顶点。
void Prim(Graph* g, int parent[]) {
int key[MAXVERTICES], visited[MAXVERTICES] = {0};
for (int i = 0; i < g->vertices; i++) {
key[i] = INF;
}
key[0] = 0;
parent[0] = -1;
for (int count = 0; count < g->vertices - 1; count++) {
int u = -1;
for (int i = 0; i < g->vertices; i++) {
if (!visited[i] && (u == -1 || key[i] < key[u])) {
u = i;
}
}
visited[u] = 1;
for (int v = 0; v < g->vertices; v++) {
if (g->matrix[u][v] && !visited[v] && g->matrix[u][v] < key[v]) {
key[v] = g->matrix[u][v];
parent[v] = u;
}
}
}
}五、数据处理应用实例
图的数据处理在实际应用中非常广泛。例如,在社交网络分析中,可以使用BFS查找用户之间的最短关系链;在交通网络中,Dijkstra算法可以计算最短行车路线;在通信网络设计中,Prim算法可用于构建成本最低的网络连接。
六、
在C语言中处理图数据需要熟练掌握图的表示方法及基本算法。邻接矩阵和邻接表各有优劣,应根据具体应用场景选择。遍历、最短路径和最小生成树算法是图数据处理的核心,理解这些算法的原理和实现对于解决实际问题至关重要。通过合理的数据结构和算法设计,可以高效地处理复杂的图数据,满足各类应用需求。
参考文献
[1] Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms. MIT Press.
[2] Weiss, M. A. (2013). Data Structures and Algorithm Analysis in C. Pearson.